While quantum teleportation is primarily seen as a way of moving quantum information around, it can also make certain kinds of quantum operations simpler. Typically, in a quantum computer, some types of operation that you need to perform will be relatively easy, while others will be much harder. Since the task as a whole is quite difficult, any simplification at all can be useful.
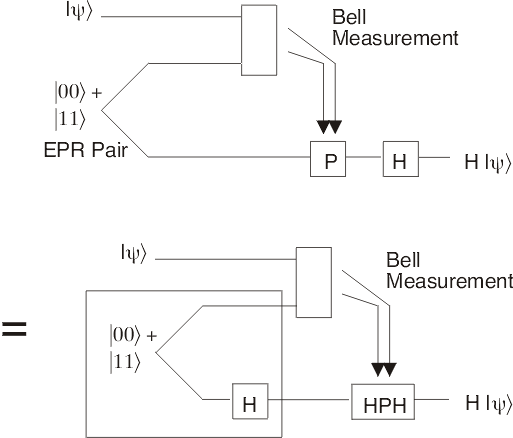
To see how quantum teleportation can provide such a simplification, consider first teleporting a qubit from Alice to Bob, then having Bob perform a basic operation like a Hadamard transform H on the qubit. (A Hadamard transform is a simple one-qubit operation that rotates the qubit into a superposition state; or it can cause interference if the qubit is already in a superposition.) In the figure below, time moves from left to right, and each line represents a qubit; the operation P performed by Bob on the lower line depends on the two classical bits he received from Alice during the teleportation step.

Now, both P and H are single-qubit gates, so performing P and then H is exactly equivalent to performing H followed by another gate P' (which is equal to HPH; H is its own inverse). But the Hadamard rotation bears a special relationship to the four possible gates P: replacing P with HPH is equivalent to rearranging the four values of the two bits sent by Alice. In other words, this new procedure (Bob performs H, then P') is no more difficult than the old one.
In fact, if P (or rather P') is easier to do than H, the new procedure is simpler: since H is now being performed directly on the EPR pair, which is a standard "ancilla" state, we can afford to do it in a way that might fail. If it fails, the state might be destroyed, but that's OK; we can try again and again until we succeed. We can't afford to do that with the data in a quantum computer -- it would be too likely that some gate along the way would fail, and then we would have to start over, since it is not possible to copy quantum information to make a backup.
While in most cases, the H gate is no harder than the P gates, there are a number of other quantum gates which bear a similar relationship to the P gates: in particular, we can consider gates for which U is hard, but UPU-1 is easy. In that case, we can push the difficult U gate off into a separate known ancilla state, possibly simplifying the task of performing U on quantum data. For instance, this type of procedure is very helpful in designing fault-tolerant quantum protocols.
For further information:
Back to Daniel Gottesman's home page
Created October 19, 2001