The 3-body problem in Shape Space (1)
The zero energy, zero angular momentum 3-body problem has two main kinds of behaviors: the dynamical orbits that end up in a three-body collision (or a three-body escape), and the ones that end up with a tight Keplerian pair plus a third particle that flies away (hyperbolic-elliptic escape). Curiously, the three-body collisions (and the corresponding escapes to infinity), can only happen in one out of four special configurations of the particles: either they form an equilateral triangle, or they are collinear, with the relative distances in one of three paticular ratios. These are called Euler configurations. This fact can be easily explained with the equivalent formulation of the 3-body problem as a dissipative system on Shape Space S.
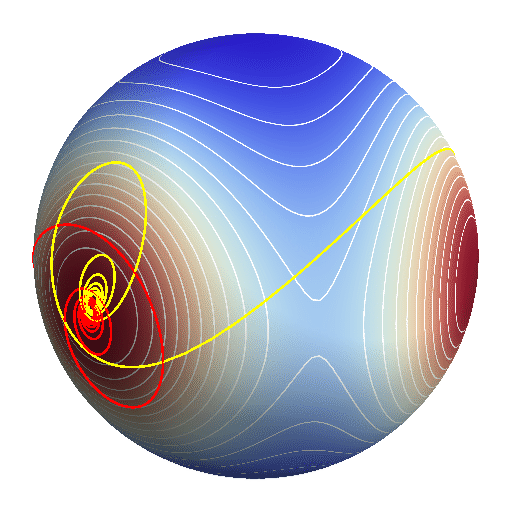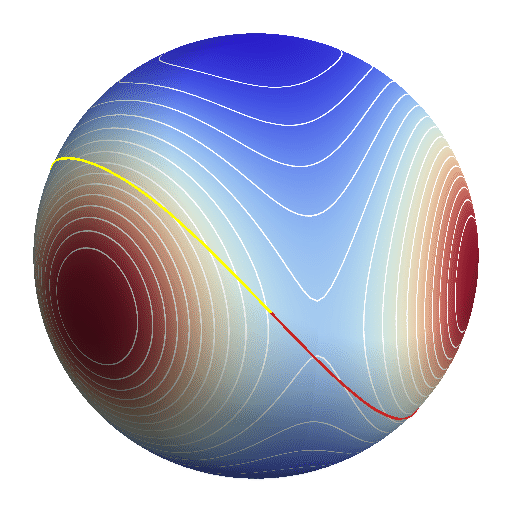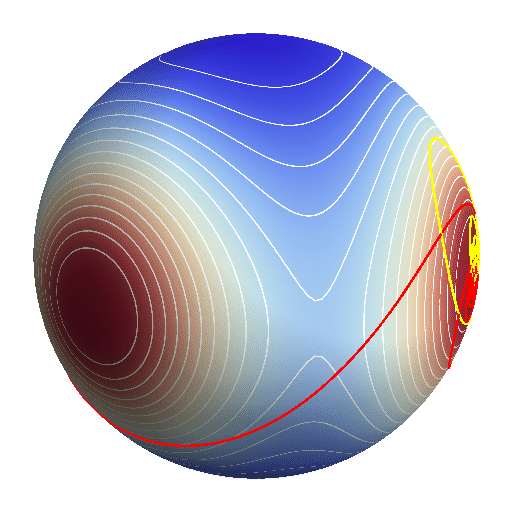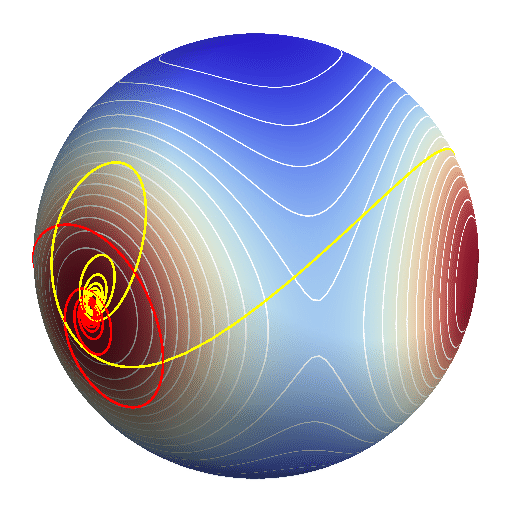 The scale-invariant Newtonian potential Vs has only five
stationary points on S: the two equilateral triangles (one
is the mirror image of the other), and the three Euler
configurations. These points are unstable equilibria of the
dynamics (the formers are maxima of Vs, the latters saddle
points). Therefore there are some special dynamical curve on S
that can end up in those points with zero momenta, and stay there
forever. In the logarithmic time this can only happen in the
infinite future of those dynamical curves, as the corresponding
arrow of time always points towards those equilibria. The
corresponding Newtonian description will be that of a three-body
collision or explosion, depending on whether Newtonian time has
the same arrow as the logarithmic time. A degenerate case is when
the representative point in S just stays forever at one of
the equilibria. The corresponding Newtonian description is that of
a homothetic fall to the center or explosion, again according to
the sign of t. All of the situations we have described so far are
a subset of measure zero of the solutions of the problem. The vast
majority of them end up in a hyperbolic-elliptic escape, which
we'll describe now,
The scale-invariant Newtonian potential Vs has only five
stationary points on S: the two equilateral triangles (one
is the mirror image of the other), and the three Euler
configurations. These points are unstable equilibria of the
dynamics (the formers are maxima of Vs, the latters saddle
points). Therefore there are some special dynamical curve on S
that can end up in those points with zero momenta, and stay there
forever. In the logarithmic time this can only happen in the
infinite future of those dynamical curves, as the corresponding
arrow of time always points towards those equilibria. The
corresponding Newtonian description will be that of a three-body
collision or explosion, depending on whether Newtonian time has
the same arrow as the logarithmic time. A degenerate case is when
the representative point in S just stays forever at one of
the equilibria. The corresponding Newtonian description is that of
a homothetic fall to the center or explosion, again according to
the sign of t. All of the situations we have described so far are
a subset of measure zero of the solutions of the problem. The vast
majority of them end up in a hyperbolic-elliptic escape, which
we'll describe now,